Optimización del suministro energético en sistemas descentralizados. • CASADOMO

Comunicación presentada al I Congreso Edificios Inteligentes:

Autores

Jorn Klaas Gruber, Instituto IMDEA Energía
José Luis Mínguez Fernández, Instituto IMDEA Energía
Milan Prodanovic, Instituto IMDEA Energía

Resumen

En los últimos años, el sector de la energía ha sufrido una importante transformación como resultado del progreso tecnológico y el desarrollo socio-económico. La integración de fuentes de energía renovable obliga a una transición gradual desde el modelo de negocio tradicional, basado en grandes plantas de producción, a una generación de energía más descentralizada. En este trabajo se presenta un enfoque para determinar el mix de suministro energético óptimo para instalaciones de pequeño y mediano tamaño. El algoritmo de optimización considera tanto la demanda eléctrica como la calorífica y determina la configuración óptima de fuentes de energía minimizando un índice económico. El enfoque propuesto proporciona un alto grado de flexibilidad y puede ser usado para estudiar la influencia de los precios de la energía en las diferentes configuraciones de suministro energético. El comportamiento del algoritmo de optimización propuesto se ilustra por los resultados obtenidos mediante un ejemplo simulado.

Introducción

La prosperidad de las sociedades modernas está íntimamente ligada a la disponibilidad de la energía y el suministro continuo es un factor clave para el desarrollo industrial. La creciente demanda de combustibles fósiles con la consecuente disminución de las reservas, sumado al elevado coste de las tecnologías de extracción modernas, hacen incrementar notablemente los precios de la energía. El impacto ambiental de los combustibles fósiles, así como los riesgos relacionados con la generación de energía nuclear, dieron lugar a una discusión sobre los efectos de la producción de energía tradicional. Estos inconvenientes llevaron en los últimos años a un aumento en investigación y desarrollo de fuentes alternativas de energía.

El aumento significativo en la integración de fuentes de energía renovables en el modelo energético actual, especialmente turbinas eólicas y paneles solares fotovoltaicos, pone de manifiesto el cambio de una producción energética centralizada con unas pocas grandes plantas de producción eléctrica hacia una generación más distribuida. La producción de energía cerca del lugar de consumo reduce las pérdidas por transmisión, aumenta la eficiencia y ayuda a asegurar una alta calidad en el suministro de energía.

Hoy en día, los edificios contribuyen fuertemente a la demanda total de energía y representan en algunos países hasta el 45% del consumo de energía primaria (Pérez-Lombard et. al, 2008). Un mix energético adecuado, especialmente el uso de fuentes de energía renovables, y un sistema de suministro óptimo pueden mejorar la eficiencia energética de los edificios y reducir los costes. En (Lozano et. al, 2009) se determina el suministro de energía óptimo para edificios del sector terciario y los algoritmos presentados en (Weber & Shah, 2011; Buoro et. al, 2013) permiten calcular la combinación óptima de fuentes energéticas para un distrito industrial o una ciudad pequeña, incluyendo el impacto ambiental del sistema de suministro de energía. En (Prodanovic et. al, 2012) se ha presentado un enfoque integrado para mejorar la eficiencia energética usando una gestión proactiva de la energía. En (Jonghe et. al, 2011) se determina la configuración óptima de tecnologías en presencia de altos niveles de energía eólica.

En este trabajo se presenta un método para determinar la configuración óptima de suministro de energía para pequeños y medianos edificios, atendiendo a perfiles estacionales de demanda eléctrica y calorífica. El objetivo se centra en la optimización de la generación distribuida de energía en combinación con baterías eléctricas y conexión a la red.

Descripción del problema Este trabajo presenta una propuesta para determinar el mix óptimo de suministro de energía para un pequeño o mediano edificio minimizando un índice económico:

Fórmula 1: J(x) = J_e(x_e) + J_h(x_h) + J_b(x_b)

donde x ∈ R^N es el vector con las capacidades iniciales instaladas y N es el número total de fuentes energéticas consideradas en la función del coste. Los términos J_e(x_e), J_h(x_h), J_b(x_b) representan los costes relacionados con las fuentes de energía eléctrica, las fuentes de calor y la batería, respectivamente. El vector de capacidades usado en (1) está definido como x^T= [x^T_e,x^T_h,x_b] con las capacidades x_e de las fuentes de generación eléctrica, x_h de las fuentes caloríficas y x_b de la batería.

El coste J_e(x_e) relacionado con las fuentes de electricidad se define como:

Fórmula 2: J_e(x_e) = J_e,_f(x_e) + J_e,_v(x_e)

siendo J_e,_f(x_e) los costes fijos anuales y J_e,_v(x_e) los costes variables dados por:

J_e,_f(x_e) = Σ^N_e_i=1X⁽ⁱ⁾_eI⁽ⁱ⁾_e/y⁽ⁱ⁾_{e ,} J_e,_v(x_e) = Σ^N_e_i=1X⁽ⁱ⁾_eρ⁽ⁱ⁾_e+ s_eρ_e

donde x⁽ⁱ⁾_e , I⁽ⁱ⁾_e e y⁽ⁱ⁾_e son las capacidades instaladas, los costes de inversión iniciales necesarios por capacidad instalada y la vida útil de la i-ésima fuente de electricidad, respectivamente. La variable x⁽ⁱ⁾_e representa la energía producida por la i-ésima fuente de electricidad durante un año y p⁽ⁱ⁾_e es el precio por unidad de energía. En el coste variable se considera la carencia de energía como término adicional donde s_e es la cantidad de energía que falta y ρ_e representa el coste de penalización por cada unidad que falta.

En el caso del calor, el coste viene dado por:

Fórmula 3: J_h(x_h) = J_h,_f(x_h) + J_h,_v(x_h)

con los costes fijos anuales J_h,_f(x_h) y los costes variables J_h,_v(x_h) definidos como:

J_h,_f(x_h) = Σ^N_h_i=1X⁽ⁱ⁾_hI⁽ⁱ⁾_h/y⁽ⁱ⁾_h, J_h,_v(x_h) = Σ^N_h_i=1X⁽ⁱ⁾_hρ⁽ⁱ⁾_h+ s_hρ_h

donde x⁽ⁱ⁾_h , I⁽ⁱ⁾_h e y⁽ⁱ⁾_h son las capacidades instaladas, las inversiones iniciales por potencia instalada y la vida útil de la i-ésima fuente de calor, respectivamente. La variable x⁽ⁱ⁾_h representa la cantidad de energía generada durante un año por la i-ésima fuente de calor y p⁽ⁱ⁾_h es el precio por unidad de energía. Además, los costes variables consideran el caso de que exista un déficit, donde s_h indica la cantidad de calor que falta y ρ_h es la penalización por cada unidad de energía que falta.

Para la batería, el coste se define como:

Fórmula 4: J_b(x_b) = J_b,_f(x_b) + J_b,_v(x_b)

con los costes fijos J_b,_f(x_b) y variables J_b,_v(x_b) dados por:

J_b,_f(x_b) = x_bI_b/y_{b ,} J_b,_v(x_b) = Σ^N_e_i=1X⁽ⁱ⁾_bp⁽ⁱ⁾_e

donde x_b indica la capacidad de la batería instalada, l_b representa la inversión inicial necesaria por capacidad de almacenamiento e y_b es la vida útil de la batería. Los costes variables dependen de la cantidad de energía X⁽ⁱ⁾_b de las fuentes eléctricas usadas para cargar la batería y el precio correspondiente p⁽ⁱ⁾_e por unidad de energía.

Optimización

El objetivo de la optimización consiste en minimizar los costes de la energía (1) asociados a cierta demanda eléctrica y calorífica. El uso de múltiples perfiles de demanda permite tener en cuenta las variaciones de la misma durante un año, además proporciona una estimación más realista de los costes de la energía.

Minimización del coste

La energía generada (X⁽ⁱ⁾_e, X⁽ⁱ⁾_h e X⁽ⁱ⁾_b) y la energía que falta (s_e y s_h) pueden ser calculadas con los procedimientos de asignación presentados en (Gruber et. al, 2013). Las inversiones iniciales (I⁽ⁱ⁾_e, I⁽ⁱ⁾_h e I_b), los tiempos de vida útil (y⁽ⁱ⁾_e, y⁽ⁱ⁾_h e y_b), los precios por unidad de energía (p⁽ⁱ⁾_e y p⁽ⁱ⁾_h) y los costes por cada unidad de energía que falta (ρ_e y ρ_h) son parámetros constantes y conocidos. Las ecuaciones (2), (3) y (4) permiten determinar los costes asociados a las fuentes eléctricas, las fuentes de calor y la batería, respectivamente. Finalmente, con los costes de las diferentes fuentes se puede calcular el coste total (1) del suministro de energía.

Ahora, las capacidades óptimas x_* de las fuentes de energía se calculan resolviendo el siguiente problema de minimización con restricciones:

x_* = arg min J(x)
x
s.t. Ax<b

con AE R^NcxN y b E R^Nc donde N_c denota el número de restricciones. El problema de optimización puede ser resuelto con programación no lineal (NLP).

Implementación y resultados

El enfoque propuesto para la minimización del coste relacionado con el suministro de energía de edificios de pequeño y mediano tamaño ha sido implementado en Matlab. Las capacidades óptimas se calculan resolviendo el problema de minimización con la función incorporada de Matlab para la programación cuadrática secuencial (fmincon).

Implementación

Para la satisfacción de la demanda eléctrica se han considerado turbinas eólicas, sistemas fotovoltaicos, turbinas de gas, plantas de microcogeneración (CHP), conexión a la red y baterías. Las bombas de calor, calderas de gasóleo, CHP, colectores termosolares y calderas de biomasa han sido tenidas en cuenta para la generación de calor.

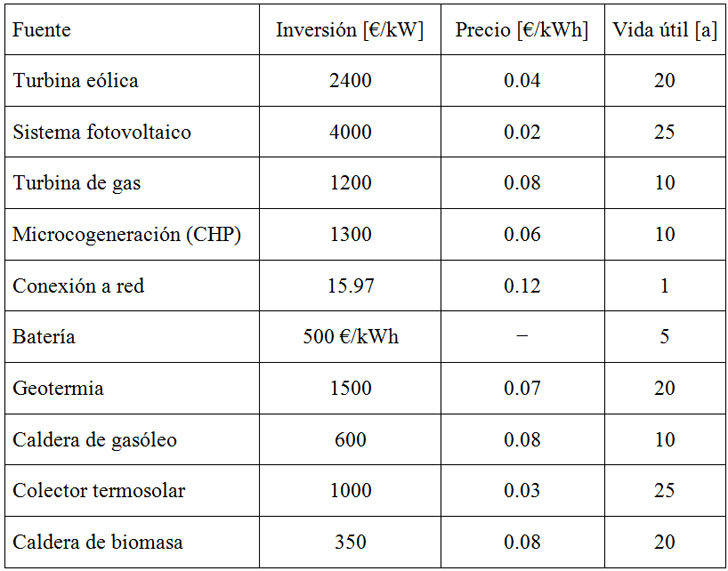
Los tiempos de vida útil, las inversiones iniciales por unidad de capacidad y los precios por unidad de energía de las fuentes energéticas se dan en la Tabla I. En el caso de un déficit de energía, se usa una penalización de ρ_e = ρ_h = 1000 €/kWh tanto para la electricidad como para el calor. Para las turbinas eólicas se ha supuesto un rendimiento del 30 % y para los sistemas de microcogeneración la proporción electricidad/calor está dada por la relación 0.3/0.7.

Figura 1. Vida útil, inversiones por capacidad y precios de energía de las fuentes consideradas.

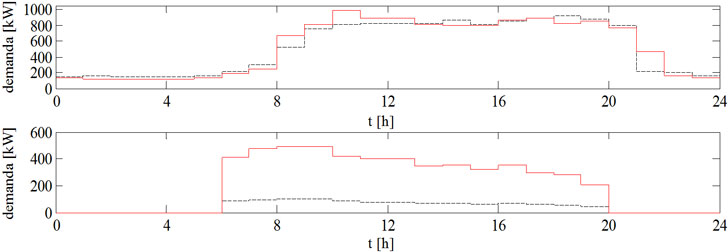
Demanda eléctrica y calorífica — Figura 2. La demanda eléctrica (arriba) y calorífica (abajo) en invierno (línea continua) y verano (línea discontinua).

Se han utilizado para el edificio de oficinas de tamaño medio ubicado en Madrid dos perfiles de demanda (véase la Figura 2), uno para invierno y otro para verano, El procedimiento de optimización del mix de suministro de energía considera medio año de verano y medio año de invierno.

Resultados

El procedimiento propuesto se ha usado para determinar la configuración óptima de suministro de energía del edificio de oficinas. Los costes han sido optimizados usando los precios actuales de energía (ver Figura 1) para cada una de las fuentes.

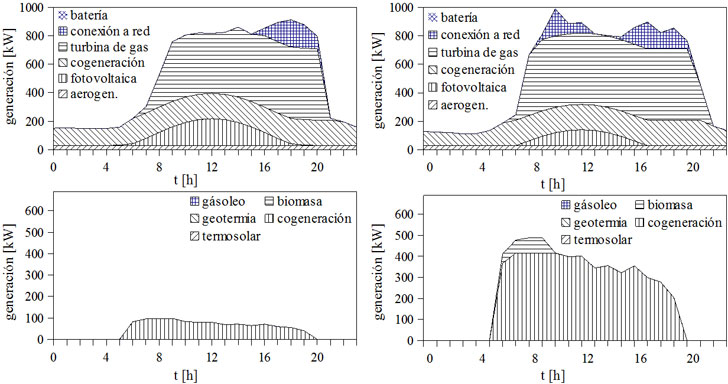
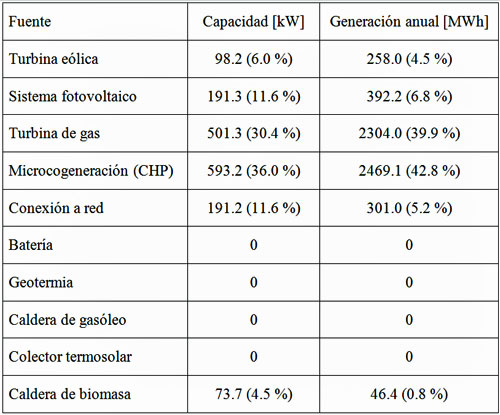
Los resultados obtenidos para el consumo de energía que se dan para los perfiles de verano e invierno se muestran en la Figura 3. Se puede ver que la mayor parte de la demanda de electricidad y de calor está cubierta por las fuentes de energía fósil y sólo una proporción reducida se satisface con la energía renovable. Por otra parte, algunas de las tecnologías disponibles no están incluidas en el mix energético óptimo (baterías, bombas de calor geotérmicas, colectores termosolares y calderas de gasóleo) por razones económicas. Las capacidades de las fuentes de energía y la cantidad de energía producida por cada fuente se dan en la Figura 4. Con los precios actuales, el 82.7 % de la demanda energética se cubre con combustibles fósiles, el 5.2 % se extrae de la red y el 12.1% proviene de fuentes de energía renovables.

Producción eléctrica y calor — Figura 3. Producción eléctrica (arriba) y de calor (abajo) en verano (izquierda) e invierno (derecha).

Figura 4. Capacidades de las fuentes energéticas y cantidad de energía producida durante un año.

Con la reducción de precios prevista de las fuentes de energía renovables y el aumento de los precios de los combustibles fósiles, la generación descentralizada será más importante en el futuro. Además, se espera que las mejoras en las tecnologías de almacenamiento refuercen el uso de baterías y otros sistemas de acumulación.

Conclusiones

Se ha desarrollado e implementado un procedimiento para el cálculo del mix de suministro óptimo para los sistemas descentralizados de energía. El enfoque presentado minimiza una función objetivo de la demanda de energía dada usando las reglas económicas básicas. El uso de múltiples perfiles permite considerar las variaciones estacionales en la demanda de electricidad y calor. El algoritmo descrito ha sido implementado en Matlab considerando diez fuentes de energía, incluidas las baterías y los sistemas de cogeneración. La optimización considera los costes de capital y los costes variables resultantes de la producción de energía. Además, el algoritmo propuesto permite incluir fácilmente otros costes relacionados con el desmantela-miento, la gestión de residuos, transporte de CO2 y almacenamiento con el fin de obtener una optimización más diferenciada y su posterior análisis del mix de suministro.

La configuración óptima de suministro de energía para un edificio de oficinas de medio tamaño que se encuentra en Madrid (España) se determinó utilizando el procedimiento de optimización propuesto. Los resultados obtenidos muestran un predominio de la producción de energía a partir de combustibles fósiles según los precios actuales del mercado y un menor uso de energía renovable. La alta flexibilidad del procedimiento permite estudiar los cambios en el suministro de energía óptimo en función de los costes de inversión y los precios de la energía.

Referencias

Buoro, D., Casisi, M., De Nardi, A., Pinamonti, P. & Reini, M., 2013, Multicriteria optimization of a distributed energy supply system for an industrial area, Energy, 58: 128-137.
De Jonghe, C., Delarue, E., Belmans, R. & D’haeseleer, W., 2011, Determining optimal electricity technology mix with high level of wind power penetration, Applied Energy, 88(6): 2231-2238.
Gruber, J.K., Mínguez Fernández, J.L. & Prodanovic, M., 2013, Supply mix optimization for decentralized energy systems, 2013 International Conference on Smart Grid, Pekín, pp. 5-11.
Huld, T., Müller, R. & Gambardella, A., 2012, A new solar radiation database for estimating PV performance in Europe and Africa, Solar Energy, 86(6): 1803-1815.
Lozano, M.A., Ramos, J.C., Carvalho, M. & Serra, L. M., 2009, Structure optimization of energy supply systems in tertiary sector buildings, Energy and Buildings, 41(10): 1063-1075.
Pérez-Lombard, L., Ortiz, J. & Pout C., 2008, A review on buildings energy consumption information, Energy and Buildings, 40(3): 394-398.
Prodanovic, M., Gafurov, T. & Téllez, M.B., 2012, A Demand Based Approach to Optimisation of Energy Supply Mix for Smart Buildings, 2012 IEEE PES Innovative Smart Grid Technologies Conference, Washington, pp. 1-8.
Weber C. & Shah N., 2011, Optimisation based design of a district energy system for an eco-town in the United Kingdom, Energy, 36(2): 1292-1308.